Поможем написать любую работу на аналогичную тему
1. Если проводить серию измерений исследуемой величины и определить среднее арифметическое (среднее) значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов измерения от истинного значения величины в сторону уменьшения и увеличения (в том случае, когда систематическая погрешность равна нулю). Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического значения большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.
2. Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений. Эти статистические закономерности справедливы лишь при многократном повторении измерений (
). После обработки результатов измерений, получается не абсолютно достоверный, а наиболее вероятный результат и этим результатом будет среднее арифметическое значение ряда измерений (в дальнейшем эту величину будем называть также математическим ожиданием 
результатов измерений).
где n- число измерений. Тогда 
.
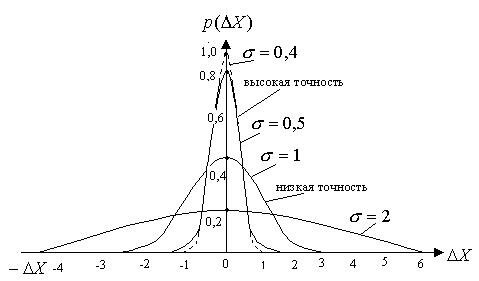
где 
- плотность вероятности случайной погрешности 
-параметр, характеризующий степень случайного разброса результатов отдельных измерений относительно истинного значения Х (в дальнейшем так же будем называть средним квадратическим или стандартным значением).
где 
- численный результат отдельного измерения, а 
- число измерений.
 |
(35)
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0,4 |
0,4 |
0,6 |
0,8 |
0,14 |
1,2 |
0,01 |
|
0,5 |
0,5 |
0,49 |
1,0 |
0,11 |
1,5 |
0,0089 |
|
1,0 |
1,0 |
0,24 |
2,0 |
0,05 |
3,0 |
0,0045 |
|
2,0 |
2,0 |
0,12 |
4,0 |
0,03 |
6,0 |
0,0022 |
 |
Рис.12
сводится к виду
где 
- абсолютная погрешность единичного ряда n- измерений,
1. получено n измерений одной величины 
2. определяется среднее арифметическое этого ряда 
3. вычисляются абсолютные погрешности каждого измерения 
4. определяется среднеквадратическое средних арифметических значений (хотя и не производятся серии повторных измерений)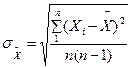 
5. определяется коэффициент Стьюдента для заданного числа измерений, например n=8 и доверительной вероятности, например P=0,95
|
|
|||||||||
|
0,50 |
0,80 |
0,95 |
0,98 |
0,99 |
1,00 0,68 0,67 |
3,08 1,31 1,28 2,04 1,96 |
31,82 2,46 2,33 |
63,66 2,75 2,58 |
|
, если 50n
7. измеряется ряд значений следующей физической величины и повторяется статистическая обработка этого ряда измерений (п.1
п.6)
| Предыдущие материалы: | Следующие материалы: |