Поможем написать любую работу на аналогичную тему
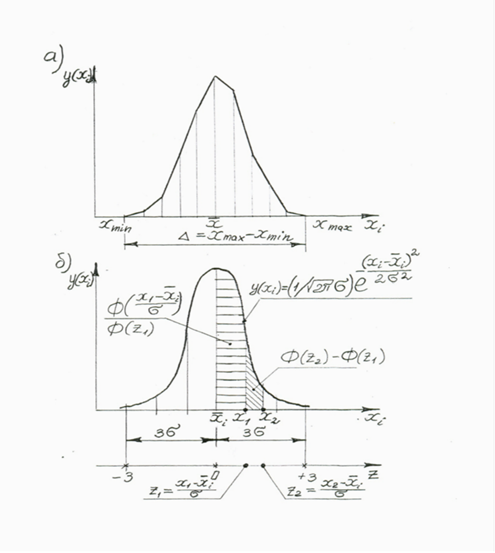
Рисунок 1 — а) полигон распределения значений хi;
б) теоретическая кривая распределения значений случайной величины хi
Характер эмпирических значений случайной величины (см. рис. 1а) часто соответствует теоретическому закону — нормальному закону (или закону Гаусса) (рисунок 1б). Для этого закона плотность вероятности у(х) характеризуется функцией (см. рисунок 1 б):
(1.7)
где σ — средняя квадратичная ошибка измерения, хi — действительное (текущее) значение физической величины, i — среднее значение величины.
Эта зависимость возникает, если на случайную величину оказывает влияние большое количество факторов, ни один из которых не является превалирующим. Соответствие эмпирического распределения, показанного на рисунке 1а предполагаемому теоретическому закону проверяется с помощью различных критериев: хи-квадрат χ2, критерии Колмогорова, Пирсона и др.
Кроме нормального закона в теории погрешностей используют и другие законы: равновероятный, биномиальный, пуассоновский, гипергеометрический и др. .
Из графика нормального закона следует (см. рисунок 1б):
- наиболее часто при измерениях встречаются значения, близкие к среднему значению i ,
- чем больше отличаются значения от среднего, тем реже они встречаются. Среднее значение (математическое ожидание) i характеризует условно «истинное» значение. Другие же значения при измерениях появляются под влиянием случайных ошибок. Чем больше значение отличается от среднего, тем больше ошибка измерения, тем реже она встречается.
Теоретически кривая нормального распределения (рисунок 1б) располагается от -∞ до +∞, но действительные значения, существенно отличающиеся от среднего, встречаются относительно редко. Поэтому для практических целей принимают, что диапазон изменений действительных значений составляет 6σ или ±3σ. Таким образом, в пределах ±3σ будет находиться 99,73% всех действительных значений, т.е. вероятность получения значения физической величины в пределах х ±3σ равна 0,9973. Вероятность получения значения, отстоящего от среднего («истинного») значения более, чем на 3σ , мала и составляет (1-0,9973)/2=0,00135.
| Предыдущие материалы: | Следующие материалы: |