Системы допусков и посадок

Главная страница ---> Лекции по нормированию точности и техническим измерениям ---> Системы допусков и посадок

Систематизация и классификация используются как мощный инструмент познания. Изучение некоторой системы объектов всегда основано на выделении их наиболее существенных и общих свойств. Такое упорядочение информации позволяет установить ее необходимый минимум для грамотного использования в конкретной области. Кроме того, любая классификация проявляет “белые пятна” и способствует их заполнению, т.е. совершенствованию самой системы. Систематизация широко применяется в любой области науки и техники, а в стандартизации она является одним из важнейших рабочих инструментов.

Анализ любых технически сложных изделий позволяет выявить многократно повторяющиеся типовые сопряжения и поверхности деталей, которые должны быть стандартизованы. Стандартизованы точность геометрических параметров подшипников, зубчатых колес и передач, рабочих и контрольных калибров и т.д. Можно говорить о системах нормирования стандартных требований к точности таких объектов. При этом следует различать системы допусков и системы допусков и посадок.

Для несопрягаемых элементов и для отдельно рассматриваемых поверхностей разрабатывают системы допусков. Есть, например, системы допусков углов, системы допусков формы и расположения поверхностей и ряд других. Там где нужны стандартные сопряжения поверхностей, стандартизаторы разрабатывают системы допусков и посадок. Стандартные системы допусков и посадок включают системы для гладких цилиндрических и приравниваемых к ним поверхностей, системы для резьбовых, шпоночных и шлицевых сопряжений и ряд других.

Формы и содержание систем допусков, а также систем допусков и посадок весьма разнообразны и потому непосредственное их сопоставление затруднительно. Правильное использование норм точности различных поверхностей и сопряжений подразумевает знание каждой конкретной системы. Изучение всех систем порознь требует слишком большого времени из-за огромного количества фактического материала. Рационализация изучения систем допусков и посадок возможна за счет отсеивания маловажных подробностей и концентрации внимания на основном содержании. Понятно, что анализ каждой системы допусков и посадок должен привести к выделению аналогичных “скелетов”, если стандартизаторы правильно подошли к разработке систем. Анализ множества систем допусков и посадок подтверждает, что они построены единообразно, на некоторых общих принципах, которые рассмотрены ниже.

В системах допусков и посадок можно обнаружить следующие общие принципы построения:

принцип предпочтительности;

принцип измерений при нормальных условиях;

принцип ограничения предельных контуров;

принцип формализации допусков;

принцип увязки допусков с эффективными параметрами;

принцип группирования значений эффективных параметров;

принцип установления уровней относительной точности.

Рассмотрим представленные принципы более подробно.

Принцип предпочтительности – один из основных принципов, используемых в стандартизации. Назначение этого принципа состоит в создании необходимого разнообразия стандартных решений при ограничении использования их номенклатуры. Если вся номенклатура стандартных решений рассчитана на обеспечение всех, в том числе и сравнительно редко встречающихся задач, то типовые решения наиболее часто встречающихся задач рассматриваются как более предпочтительные для использования. В результате из множества возможных стандартных решений наиболее часто применяют их ограниченное число, что благоприятно сказывается на уменьшении номенклатуры назначаемых норм.

Различают качественный и количественный аспекты применения принципа предпочтительности. Качественная сторона этого принципа состоит в образовании предпочтительных рядов объектов стандартизации. Объектами могут быть конкретные изделия, детали, их конструктивные элементы, посадки, допуски и т.д.

Предпочтительных рядов может быть как минимум два, причем всегда устанавливаются уровни предпочтительности. В соответствии с этими уровнями следует выбирать стандартные объекты. Как правило, наиболее предпочтительный ряд включает наименьшее количество объектов стандартизации. Следующие, менее предпочтительные ряды, обычно отличаются расширенной номенклатурой и могут включать объекты предыдущих рядов. Соблюдение принципа предпочтительности позволяет добиться разумного сокращения применяемой номенклатуры стандартных объектов. В первую очередь следует применять номенклатуру наиболее предпочтительного ряда и переходить к выбору из менее предпочтительных только тогда, когда поставленная задача на более высоком уровне предпочтительности не имеет удовлетворительного решения.

В стандартных системах допусков и посадок обычно устанавливают ряды с несколькими уровнями предпочтения, например, предпочтительные посадки (первый уровень), рекомендуемые посадки (второй уровень), и, наконец, все стандартные посадки (третий, самый низкий уровень предпочтительности).

Количественная сторона принципа предпочтительности реализуется через использование рядов предпочтительных чисел. В машиностроении эти ряды построены на основе геометрической прогрессии, знаменателем которой является корень определенной степени из десяти (такие ряды называют рядами R или рядами Ренара). Ряды R5… R40 называют основными, ряд R80 – дополнительным.

Предназначение рядов предпочтительных чисел состоит в том, что их использование обеспечивает упорядочение и определенный экономический эффект при выборе числовых значений любых параметров, на которые нет конкретного нормативного документа (НД) по стандартизации. При стандартизации параметрических рядов и пересмотре действующих НД также необходимо использование предпочтительных чисел и их рядов. Стандартизуемые и нормируемые параметры могут иметь разный характер, но при выборе их номинальных значений из рядов предпочтительных чисел значительно легче согласуются между собой изделия, предназначенные для работы в одной технологической цепочке, или являющиеся объектами технологического процесса. Например, использование транспортных и грузоподъемных средств будет достаточно рациональным, если грузоподъемность и массы грузов будут построены по ряду R5, т.е. грузоподъемность железнодорожных вагонов будет составлять 25 т, 40 т, 63 т, и 100 т, вместимость (грузоподъемность) контейнеров – 250 кг, 400 кг, 630 кг, 1000 кг, масса ящиков – 25 кг, 40 кг, 63 кг и 100 кг, масса коробок или банок – 250 г, 400 г, 630 г и 1000 г.

Стандарт ГОСТ 8032-84 устанавливает порядок применения рядов предпочтительных чисел, включая образование производных рядов. Они могут образовываться отбором каждого n-ного члена основного ряда; можно также составлять ряды с неодинаковыми знаменателями в различных диапазонах. Таким образом регулируют номинальные значения членов рядов и их “густоту”.

Значение членов рядов рассчитывается с использованием приведенных выше знаменателей геометрических прогрессий. Значения знаменателей рядов предпочтительных чисел и самих чисел округлены по сравнению с точными значениями геометрических прогрессий. Свойства рядов предпочтительных чисел соответствуют свойствам геометрической прогрессии. Наиболее предпочтительным является ряд R5, за ним следует ряд R10, и т.д. Дополнительный ряд R80 можно применять только в технически и экономически обоснованных случаях.

Количество членов каждого ряда предпочтительных чисел в любом десятичном интервале соответствует числу в обозначении ряда. В стандарте приведены значения членов рядов от 1 до 10. Значения в других диапазонах рядов рассчитывают умножением приведенных членов на 10 в соответствующей положительной или отрицательной степени. Таким образом, можно считать, что ряды предпочтительных чисел практически бесконечны в обе стороны.

Стандартизаторы при необходимости используют не только геометрическую, но и арифметическую прогрессию. Применяют также и ступенчатые арифметические ряды с отличающимися разностями в различных поддиапазонах.

В электротехнике применяют также предпочтительные числа, построенные по рядам E – геометрические прогрессии со знаменателями в виде корней третьей, шестой, двенадцатой, двадцать четвертой, сорок восьмой, девяносто шестой и сто девяносто второй степеней из десяти. Примерные значения знаменателей первых четырех рядов: Е3 – 2,2; Е6 – 1,5; Е12 – 1,2 и Е24 – 1,1.

В системах стандартов допусков и посадок ряды допусков обычно строятся с использованием рядов предпочтительных чисел. Возможны и другие проявления количественной стороны принципа предпочтительности в системах стандартов. Например, в стандарте допусков углов границы интервалов длин короткой стороны угла построены по ряду R5.

Наиболее полно принцип предпочтительности использован в стандарте, устанавливающем нормальные линейные размеры (ГОСТ 6636-69). Этот стандарт не нормирует допуски размеров, но является одним из важнейших для унификации параметров. Унифицированными геометрическими параметрами являются те, у которых одинаковы не только поля допусков, но и номинальные значения. Для унификации параметров необходимо при проектировании изделий по возможности назначать нормальные линейные размеры деталей (диаметры, толщины, глубины уступов и т.д.), выбранные с учетом уровней предпочтительности.

Необходимо учитывать, что требования стандарта не распространяются на технологические межоперационные размеры, на размеры, зависящие от других принятых значений, а также на размеры, установленные в стандартах на конкретные изделия.

Ряды нормальных линейных размеров (обозначаются буквами Rа с соответствующим числом) построены на базе рядов предпочтительных чисел. Числовые значения нормальных линейных размеров начинаются с 0,01 мм и заканчиваются значением 20 000 мм. В дополнение к геометрическим рядам стандарт содержит также арифметический ряд размеров в диапазоне от 0,001 мм до 0,009 мм с разностью в 0,001 мм. Основные ряды нормальных линейных размеров (Rа5 – Rа40) построены в соответствии с рядами R5 – R40. Ряды Rа5 – Rа40 как геометрические прогрессии с округленными значениями членов ряда. Дополнительный ряд содержит ограниченное (неполное) число членов, рассчитанных на основе ряда R80.

Принципиальные отличия рядов нормальных линейных размеров от рядов предпочтительных чисел заключаются в том, что ряды Ra размеров конечны и содержат некоторые округленные по сравнению с рядами R значения, причем в стандарт включены все значения размеров в указанном диапазоне. Некоторые отличительные особенности дополнительного ряда уже упоминались.

Два следующих принципа (принципы измерений при нормальных условиях и ограничения предельных контуров) обеспечивают инвариантность требований, устанавливаемых в системе допусков и посадок (от латинского invariantis – неизменяющийся – свойство неизменности по отношению к какому-либо преобразованию, условию, или совокупности преобразований). Под обеспечением инвариантности элементов деталей понимают такое построение систем допусков (систем допусков и посадок), которое гарантирует геометрическую взаимозаменяемость (инвариантность) деталей, изготовленных по одним и тем же требованиям к номинальным значениям и к точности геометрических параметров.

Чтобы система обеспечивала инвариантность деталей, должны соблюдаться заложенные в ней условия годности деталей: единообразие трактовки годности и достоверность результатов контроля. Только при соблюдении этих условий результаты измерений можно сопоставить с моделью годной детали, которая задана чертежом, и дать объективное заключение о годности.

Единообразие трактовки годности детали обеспечивается установлением ее предельных контуров, в которые должна “вписываться” реальная деталь. Фактические значения геометрических параметров контролируемой детали определяются по результатам измерений, причем достоверную информацию о параметрах детали можно получить только при измерении в нормальных условиях.

Несоблюдение этих принципов исключает возможность применения систем допусков и посадок. Попытки произвольной трактовки годности могут привести к возникновению конфликтных ситуаций между изготовителем и контролером. Такие же последствия возможны при нарушениях нормальных условий измерений.

Принцип измерений при нормальных условиях обеспечивает единообразие информации, получаемой при неоднократных независимых измерениях одних и тех же параметров. Измерения в нормальных условиях означают, что измерения проводят при нормальных значениях влияющих физических величин. Под влияющими величинами понимают те физические величины, которые не являются измеряемыми, но могут вызвать искажение результатов измерений из-за воздействия на сам объект измерения и/или на применяемые средства измерений. Например, при измерении длины всегда существенное значение имеет температура контролируемой детали, от которой зависит фактическое значение размера. Понятно, что температурный фактор сказывается не только на измеряемом объекте, но и на применяемых средствах измерений.

Менее очевидно влияние таких величин, как относительная влажность или давление воздуха, параметры гравитационных и электромагнитных полей и т.д. С другой стороны, непосредственное влияние электромагнитных полей на электрические средства измерений сомнений не вызывает. Поддается анализу воздействие влажности или давления на пневматические приборы или на емкостные электрические преобразователи. Не столь существенным оказывается влияние относительной влажности, атмосферного давления или гравитации на контролируемые детали.

Можно представить себе пластмассовую деталь, размер которой зависит от относительной влажности воздуха (гидрофильные пластмассы впитывают влагу и увеличиваются в размерах). Нежесткие детали деформируются под действием силы тяжести и размеры их искажаются.

Нормальные условия измерений линейных размеров предполагают колебания влияющих величин в пределах областей их нормальных значений. Под областью нормальных значений влияющей физической величины понимают такую область ее изменений, при которых погрешности, вызванные воздействием этой величины, могут быть признаны пренебрежимо малыми. Кроме нормальных условий измерений возможно также измерение параметров в рабочих условиях – в таких условиях погрешности из-за воздействия влияющих величин не превышают заранее определенных допустимых значений.

Проблема установления номенклатуры влияющих величин и областей их нормальных значений настолько сложна, что для случая измерений линейных размеров ей посвящен специальный стандарт (ГОСТ 8.050-73). Указание в некоторых стандартах допусков и посадок значения нормальной температуры в виде номинального значения (20 оС) не дает необходимой информации и может служить только формальным ориентиром.

Принцип ограничения предельных контуров необходим для соблюдения единообразия при решении вопроса о годности детали по контролируемому параметру.

Ограничение предельных контуров фактически определяет поля допусков, что необходимо для получения однозначного заключения о годности детали по результатам ее измерительного контроля. Необходимо установить правила разбраковки деталей по результатам измерений размеров элемента в нескольких сечениях. Формальным основанием для разбраковки деталей по размерам является истолкование предельных контуров детали. Деталь признается годной в том случае, если ее реальные контуры, установленные по результатам измерений, не выходят за предельные. При этом экстремальные действительные значения могут быть равны предельным.

В разных стандартах систем допусков и посадок истолкование предельных значений параметров содержится в явном виде или оформлено косвенно, через установление полей допусков. Наиболее подробно установление предельных контуров реализовано в стандартах на допуски формы и расположения поверхностей. В этих стандартах приведены описания полей допусков и методики их построения для каждого рассматриваемого случая, а также методики оценки отклонений реальных элементов от идеальной формы и расположения.

Истолкование предельных контуров для определения годности сопрягаемых поверхностей по размерам можно проиллюстрировать на примере длинного изогнутого вала (рис А 4.1). Если даже его толщина в любом сечении не выходит за предельные размеры (dmin £ di £ dmax ), но реальный профиль не вписывается в максимальный предельный контур (hmax dmax), то деталь должна быть признана бракованной. Для этого в стандарте ГОСТ 25346-89 установлены необходимые формальные основания, которые сформулированы в подразделе «Интерпретация предельных размеров».

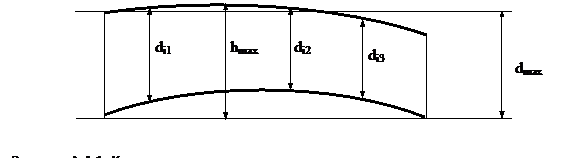В Приложении 2 (справочном) этого же стандарта говорится, что при использовании стандарта ИСО 8015 используется иная интерпретация предельных размеров (условием годности является dmin £ di £ dmax). Специфическим случаем установления предельных контуров деталей является установление только одного экстремального (наибольшего или наименьшего) предельного контура. В таком случае фактически не устанавливается допуск размера и поле допуска, поскольку отсутствует вторая граница.

Формирование рядов допусков в любой системе осуществляется на базе четырех остальных принципов. Один из них обеспечивает отделение допусков от конкретных деталей (их параметров, элементов), два следующих – возможность создавать из функционально обоснованных допусков ограниченную номенклатуру. Последний принцип направлен на обеспечение в системе необходимого разнообразия точностных требований.

Принцип формализации допусков позволяет «отделить» меру допустимого рассеяния (допуск) от поля допуска, определенным образом связанного с номинальным контуром конкретной поверхности. Абстрагирование от конкретных объектов широко используется в науке и технике. Этот прием применяется и при формализации допусков в системах.

Система допусков, в которой были бы установлены массивы предельных значений для любого номинала (все стандартные поля допусков) практически не реализуема. Значительно более удобно пользоваться рядами допусков с абстрактными значениями, “оторванными” от конкретных отклонений или предельных размеров. Такие допуски определяют только допустимые рассеяния нормируемых параметров, при этом можно задавать поле допуска имеющее любое выбранное расположение относительно номинала.

Формализованные значения допусков могут быть построены в соответствии с рядами предпочтительных чисел, и быть организованы в виде рядов с различными структурами. Например, в стандарте допусков и посадок гладких цилиндрических поверхностей ряды допусков построены в виде массива, где числовое значение допуска установлено в соответствии с интервалом номинальных размеров и уровнем точности.

В системе допусков формы и расположения поверхностей приведены несколько массивов значений допусков, в том числе допуски, связанные со значениями номинальных параметров и уровнями точности, а также абстрактный ряд допусков, построенный в порядке возрастания их числовых значений.

Одно и то же формализованное значение допуска можно использовать для интервала близких номинальных параметров, вне зависимости от расположения поля допуска по отношению к нулевой линии, которая на схеме расположения полей допусков размеров представляет номинальный размер.

Принцип увязки допусков с эффективными параметрами предназначен для расчета «теоретических значений» допусков. Формальное значение допуска не является достаточно определенной мерой точности нормируемого параметра. Представляется очевидным, что допуск в 100 мкм будет сравнительно грубым для размера 10 мм и существенно более жестким для размера 80 мм.

Чтобы обеспечить нормальную работу изделия необходимо назначить допуски требуемой точности с учетом масштабного фактора. При выборе допуска размера его значение следует связывать с номинальным размером. Выбор значения допуска угла осуществляется не в соответствии со значением углового размера, а в зависимости от длины его короткой стороны. Могут встретиться и более сложные взаимосвязи. Например, значения допусков геометрических параметров резьбовых поверхностей увязывается не только с диаметрами, но и с шагами резьбы, а для зубчатых колес допуски назначают с учетом модуля и делительного диаметра колеса. Те параметры, с которыми увязывают значения допусков, будем называть эффективными.

Увязка допуска с эффективными параметрами имеет принципиальное значение, как с конструкторских, так и с технологических позиций. Конструкторский подход к посадкам с зазором (натягом) базируется на возможности увеличивать зазор (натяг) и его допустимую неопределенность (допуск посадки) с увеличением номинального размера сопряжения. Технологический подход к возможным значениям допусков основывается на увязывании допусков с полем практического рассеяния размеров при обработке детали на определенном технологическом оборудовании. Поле рассеяния размеров при обработке каждой детали в партии зависит от множества факторов, которые будут сказываться на силовых и температурных деформациях в системе станок-приспособление-инструмент-деталь. Существенное влияние на разброс размеров в партии деталей может оказывать также износ режущего инструмента.

Из-за сложности комплексного воздействия на сопряжение, как правило, нельзя выделить один или несколько влияющих факторов и “привязать” к ним значение допуска. Поэтому эффективные параметры, с которыми увязывают значения допуска, должны отражать некоторое обобщенное влияние множества конструкторских и технологических факторов. Поэтому при построении систем допусков и посадок их разработчики вынуждены увязывать допуски с некоторыми эффективными параметрами, которые с позиций функционирования изделия (конструкторский подход) учитывают масштабный фактор при назначении норм точности размеров, а с позиций изготовления деталей (технологический подход) по возможности увязаны с точностью технологических процессов.

Функциональная зависимость допуска от эффективных параметров в общем виде может быть записана следующим образом:

Т = F(Q,V,...),

где Т – допуск параметра,

       F – знак функциональной зависимости,

      Q, V – эффективные параметры.

Из всего множества влияющих факторов отбирают те, которые характеризуют обобщенное влияние возмущений. Именно эти факторы (их может быть несколько или один) названы эффективными параметрами. Анализ систем допусков и посадок показывает, что в большинстве случаев можно обойтись одним или двумя эффективными параметрами.

Принцип группирования значений эффективных параметров используется для сокращения номенклатуры допусков в системе.

Если допуск любого параметра рассчитывать строго по функциональной зависимости, то расчетных (“теоретических”) допусков будет столько же, сколько и номинальных значений параметров. Унификация допусков и сокращение их общей номенклатуры вполне возможны за счет объединения близких значений и использования вместо них одного стандартного допуска. Различия между “теоретическими значениями” и выбранным стандартным не должны существенно искажать установленный системой допусков и посадок характер связи между значением допуска и эффективными параметрами.

Многолетняя апробация систем допусков и посадок позволила практически решить вопрос об интервалах эффективных параметров и их “представителях”. В любой системе допусков или допусков и посадок ряды допусков образованы с учетом эффективных параметров, которые сгруппированы в интервалы. Группирование осуществляется так, чтобы значения допусков на краях интервалов умеренно отличались от “теоретических”. Границы интервалов приведены в таблицах стандартов с указаниями “до” (приведенное номинальное значение включается в данный интервал) и “свыше” (приведенное значение не входит в данный интервал, и он начинается с любого большего значения).

Интервалы эффективных параметров являются одним из “входов” в таблицу рядов допусков любого стандарта.

Принцип установления уровней относительной точности обеспечивает необходимое разнообразие допусков с сохранением возможности единообразного решения типичных задач функционирования деталей и их изготовления с учетом масштабных факторов.

Для решения различных конструкторских задач необходимы допуски разной точности. Например, точность направляющих станка или измерительного прибора существенно выше точности дверного засова; подшипники шпинделя станка точнее подшипников автомобильных колес и т.д.

Понятие точности геометрических параметров не может рассматриваться как абсолютное. Известна связь допуска со значениями эффективных параметров. Следовательно, можно говорить об установлении в любой системе допусков и посадок уровней относительной точности, которые используются для назначения “одинаково точных” допусков однотипных параметров с разными номинальными значениями.

Уровни относительной точности в различных стандартных системах допусков и посадок называются по-разному. В системе допусков и посадок гладких цилиндрических поверхностей они называются квалитетами, в системах допусков формы и расположения поверхностей, допусков зубчатых колес – степенями точности. Для подшипников качения, допусков несопрягаемых поверхностей (“неуказанные допуски”) и некоторых других случаев используют понятие классов точности. Наименование уровней относительной точности зависит от конкретных объектов и сложившихся традиций.

Установленные стандартами уровни относительной точности используются как второй вход в таблицах допусков. Первым входом являются интервалы эффективных параметров, а значение допуска отыскивают на пересечении двух входов в таблицу по принципу “строка-столбец”.

Уровни относительной точности играют весьма важную роль в использовании аналогии для выбора норм точности при проектировании или технологического оборудования при разработке технологического процесса. Вне зависимости от конкретного значения нормируемого параметра можно, опираясь на уровень относительной точности, выбрать допуск (посадку) которые обеспечат удовлетворительное выполнение требуемых функций, а по уровню относительной точности параметра изготавливаемой детали – технологическое оборудование, обеспечивающее удовлетворительное поле практического рассеяния при обработке поверхности.

На использовании уровней относительной точности построены справочники конструкторов и технологов, а также значительная часть нормативно-технических документов. Уровни относительной точности фиксируются в обозначениях допусков и посадок, за исключением тех случаев, когда приводят только значения предельных отклонений.