Алгоритмы обработки многократных измерений.

Главная страница ---> Готовые ответы по метрологии и стандартизации ---> Алгоритмы обработки многократных измерений.

Последовательность обработки результатов измерений включает следующие этапы:

·исправляют результаты наблюдений исключением (если это возможно) систематической погрешности;

·вычисляют среднее арифметическое значение  по формуле

i ≈ М(х) = х i ∙ у(х i) dx ≈ (∑xi)/n

• вычисляют выборочное СКО σ  от значения погрешности измерений по формуле

                               

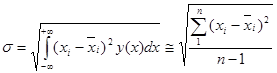
·исключают промахи;

Параметр σ характеризует точность измерений: меньше σ — выше точность измерений. Как следует из рассмотренного, наибольшая (предельная) случайная ошибка измерений ∆ lim составит приблизительно 3 σ (с вероятностью 0,9973).

                                                     

                                               ∆ lim = 3σ,                                                       (1.11)

      Обычно приборы и инструменты конструируют таким образом, чтобы цена деления прибора (наименьшее значение, отсчитываемое по целым делениям шкалы) не превышала предельной ошибки. Исключения составляют приборы для измерения больших линейных размеров, некоторые часовые механизмы и др.

·определяют закон распределения случайной составляющей;

·при заданном значении доверительной вероятности Р и числе измерений п по таблицам определяют коэффициент Стьюдента tp;

·находят границы доверительного интервала для случайной погрешности ;

      В общем случае при отсутствии систематической ошибки доверительный интервал, в пределах которого с принятой вероятностью будет находиться «истинное» значение величины, равен:

                                   

                                              хист. =  i  ± tσ ,                                                       (1.12)

·если величина  сравнима с абсолютным значением погрешности СИ, то величину Dси считают неисключенной систематической составляющей и в качестве доверитель ного интервала вычисляют величину

Если в результате измерительного эксперимента можно четко выделить составляющие q НСП, то DS определяется по ГОСТ 8.20776

или, по упрощенной формуле:  (по данным , погрешность такой замены не превышает 5,...,10%);

·окончательный результат записывают в виде =х±DS при вероятности Р.

Среднее арифметическое значение i лишь приблизительно равно математическому ожиданию («истинному» значению) и окажется равным последнему, если количество измерений будет бесконечно. Поэтому для оценки средней квадратичной ошибки σх среднего арифметического значения используют выражение:

                                                  σх =  ,                                                             (1.13)

                                             σ х =  ,                                                 (1.13а)

    Тогда границы доверительного интервала математического ожидания («истинного» значения) М величины x лежат в пределах:

                                        i  - 3σ / ≤  М ≤  i + 3σ /  ,                     (1.14)

или, в общем случае,                                            

                                            i  - t σ х ≤  М ≤  i + t σ х,                                                  (1.15)

где t — коэффициент, зависящий от принятой вероятности и закона распределения (при количестве измерений более 30 — нормальный закон, при меньшем числе измерений — закон Стьюдента).