Задача № 1  Произвести статистическую обработку ряда наблюдений измеряемой величины с учётом объёма этого ряда

Главная страница ---> Расчетно-Графическая работа «Метрология и радиоизмерения» ---> Задача № 1  Произвести статистическую обработку ряда наблюдений измеряемой величины с учётом объёма этого ряда

       Произвести статистическую обработку ряда наблюдений измеряемой величины с учётом объёма этого ряда. Выявить и исключить промахи, в результатах наблюдений выдвинув (если возможно) гипотезу о законе распределения с заданной доверительной вероятностью. Определить значение результата измерения, предполагая отсутствие систематической погрешности. Определить случайную среднеквадратическую погрешность результата измерения. Построить гистограмму результатов наблюдений. Сделать вывод о правомерности, выдвинутой ранее гипотезы.

 

Вар.	Доверит. вероятность	Набор ряда наблюдений
3	0,95	482,502,494,497,504,486,519,492,499,461,489,559,493, 491,481,510,505,490,490,502,491,476,466,506,514,522.

Решение:

1. Т.к. по условию задачи предполагается отсутствие систематической погрешности, то:

, тогда — исправленный ряд измерений

      2.  По исправленным результатам измерений  определяем их среднее арифметическое значение

                                                 

Найденное среднее арифметическое  является состоятельной, несмещенной и эффективной оценкой математического ожидания  при нормальном распределении результатов наблюдений, а также состоятельной и несмещенной оценкой при любых симметричных (относительно ) распределениях, т.е. .

1.   Оценим случайную погрешность каждого отдельного измерения:

                                                                                                                                    Если выполняется условие , то пункты 2 и 3 вычислены правильно.

   

Строим вариационный ряд

n = 26 ;  ;

                                                                                                    таблица 1

n
1	461	-35.96	1293.12
2	466	-30.96	958.52
3	476	-20.96	439.32
4	481	-15.96	254.72
5	482	-14.96	223.80
6	486	-10.96	120.12
7	489	-7.96	63.36
8	490	-6.96	48.44
9	490	-6.96	48.44
10	491	-5.96	35.52
11	491	-5.96	35.52
12	492	-4.96	24.60
13	493	-3.96	15.68
14	494	-2.96	8.76
15	497	-0.04	0.0016
16	499	2.04	4.16
17	502	5.04	25.40
18	502	5.04	25.40
19	504	7.04	49.56
20	505	8.04	64.64
21	506	9.04	81.72
22	510	13.04	170.04
23	514	17.04	290.36
24	519	22.04	485.76
25	522	25.04	627
26	559	62.04	3848.96

1. Находим СКО однократных измерений:

=                                                 

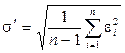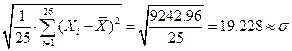
где  — оценочное значение СКО.

Очевидно, что с увеличением числа наблюдений n возрастает точность оценок  и . Разность  характеризует случайную погрешность определения математического ожидания, т.е. случайную погрешность результата n-кратного измерения. Очевидно, что случайная погрешность также имеет некоторое среднеквадратическое отклонение . Его оценка определяется соотношением

                                                                                                 

из которого следует, что результат n-кратного измерения  имеет в  раз меньше СКО по сравнению с результатом единичного измерения .

Следует иметь в виду, что если среди  результатов измерений имеются отдельные измерения, резко отличающиеся от остальных в большую или меньшую сторону, прежде всего следует проверить, не являются ли эти результаты  или  промахами, связанными с опиской, ошибкой в снятии показаний и т. п. Если промахи не установлены, следует проверить, не являются ли эти результаты грубыми погрешностями. Проверка проводится статистическим методом и сводится к сравнению нормированного отклонения  или  с максимальным маловероятным нормированным отклонением результата наблюдения , которое могло бы иметь место при данном распределении и числе наблюдений . Малая вероятность такого отклонения задается уровнем значимости , определяющим вероятность нахождения случайной величины между %-ным квантилем и . Значение  обычно выбирают от 1 до 10%. Значения  для нормального распределения при заданных  и  приведены в таблице 1

                                                                                                                                   таблица 2

	= 10%	= 5%	= 2,5%	= 1%
5 15 25 26	1,731 2,326 2,537 2,553	1,869 2,493 2,717 2,734	1,917 2,638 2,880 2,97	1,955 2,808 3,071 3,089

Если указанной отклонение проверяемого результата наблюдения оказывается больше , его следует считать грубой погрешностью, которая, как и промах, должна быть исключена их полученной совокупности результатов наблюдения. После этого следует повторить их обработку с учетом меньшего числа .

 Для   или , находим . Проведём исключение грубых ошибок

x(1) =xmin = 461, x(26) = xmax = 559

При этом: tmin= |xmin-|/σ  , tmax= |xmax-|/σ.

Проверяем:

Сравним, не является грубой ошибкой.

Сравнимявляется грубой ошибкой

 

Таким образом,  , следовательно, = 461

 не является грубой ошибкой  и остаётся в выборке;

, следовательно, = 559

 является грубой ошибкой  и исключается из выборки.

, следовательно, = 522 не является

грубой ошибкой, остаётся в выборке и становится 

Строим новый вариационный ряд, исключающий грубые ошибки, где:

    = 461=522=25 повторим  обработку результатов наблюдения с учетом меньшего числа .

    Выдвинем гипотезу о нормальном законе распределения ряда наблюдений с заданной доверительной вероятностью

- По исправленным результатам измерений  определяем их среднее арифметическое значение

                                           

Найденное среднее арифметическое  является состоятельной, несмещенной и эффективной оценкой математического ожидания  при нормальном распределении результатов наблюдений, а также состоятельной и несмещенной оценкой при любых симметричных (относительно ) распределениях, т.е. .

- Оценим случайную погрешность каждого отдельного измерения:

                                                                                                                                    

            Строим вариационный ряд                                                           таблица 3

n
1	461	-35.96	1293.12
2	466	-30.96	958.52
3	476	-20.96	439.32
4	481	-15.96	254.72
5	482	-14.96	223.80
6	486	-10.96	120.12
7	489	-7.96	63.36
8	490	-6.96	48.44
9	490	-6.96	48.44
10	491	-5.96	35.52
11	491	-5.96	35.52
12	492	-4.96	24.60
13	493	-3.96	15.68
14	494	-2.96	8.76
15	497	-0.04	0.0016
16	499	2.04	4.16
17	502	5.04	25.40
18	502	5.04	25.40
19	504	7.04	49.56
20	505	8.04	64.64
21	506	9.04	81.72
22	510	13.04	170.04
23	514	17.04	290.36
24	519	22.04	485.76
25	522	25.04	627