Случайные погрешности

Главная страница ---> Метрология, стандартизация измерительных и информационных технологий ---> Случайные погрешности

Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлением случайных погрешностей при многократно повторенных измерениях и появлением случайных событий. Из теории вероятностей известно,  что для  характеристики случайных  величин,  в нашем случае погрешностей прибора или  измерения  (вместе  с  их   систематической составляющей), необходимо определить их закон распределения.

В теории случайных погрешностей формулируются две аксиомы. Аксиома симметрии  (случайности) - при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто. Аксиома распределения - чаще всего встречаются меньшие погрешности, а большие погрешности встречаются тем реже, чем они больше.

Если эти аксиомы соблюдаются, то при неограниченном увеличении числа независимых причин,  вызывающих погрешности, мы имеем нормальный закон распределения случайной погрешности.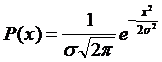

                                                                                    (2.3)

где P(х) - плотность вероятности случайной величины X; s - среднее квадратическое отклонение.

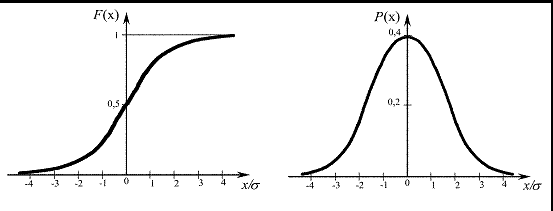
Рис. 2.1. Интегральный и дифференциальный законы распределения

Одно из  нарушений  нормального  закона распределения погрешностей при соблюдении аксиом состоит в появлении плосковершинности и  островершинности,  как показано на рис. 2.2.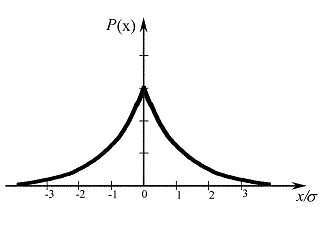

Рис. 2.2. Островершинное распределение

В пределе для плосковершинного распределения, когда уже аксиома не соблюдается, оно превращается в равномерное.

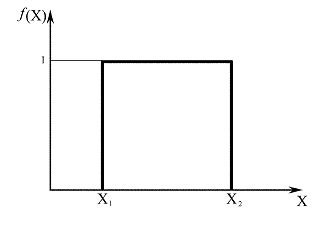
Рис. 2.3. Равномерное (равновероятное) распределение

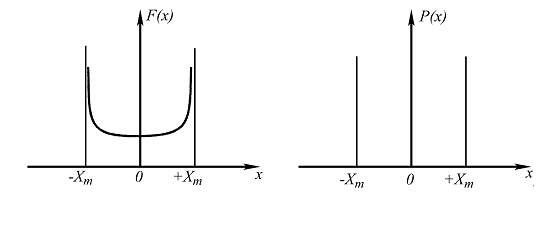
Рис. 2.4. Двухмодальное распределение

Модой дискретной случайной величины называют ее наиболее вероятное значение, а для непрерывной случайной величины модой является то значение,  при котором плотность вероятности достигает максимума. В пределе такое двухмодальное распределение  может  превратиться в распределение, когда единственно наблюдаемыми погрешностями будут только погрешности  ±XmaX  (см. рис. 2.4). Например, погрешность от люфта в кинетической цепи, погрешность от гистерезиса имеют вид двухзначной дискретной погрешности.