Доверительный интервал для истинного значения величины, имеющей нормальное распределение с известным СКО.

Главная страница ---> Ответы на экзаменационные вопросы по Метрологии, стандартизации и сертификации ---> Доверительный интервал для истинного значения величины, имеющей нормальное распределение с известным СКО.

Доверительный интервал и доверительная вероятность

Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.

Рис.1.10.

Таким образом, интервал , за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность - доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.

Доверительный интервал обычно выражают через относительную величину в долях среднего квадратического отклонения (“кратность”) . Для нормального закона доверительную вероятность определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается и определяется

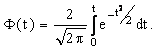
Зная доверительные границы и можно определить доверительную вероятность

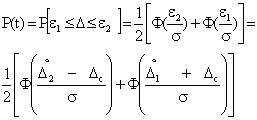
Если значения доверительных границ и симметричны, т.е.

, то и .

Тогда

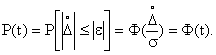
Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности.                                   Таблица 1.3

P(t)	0,90	0,95	0,99	0,999
t	1,645	1,960	2,576	3,291

При нормальном законе распределения доверительный интервал имеет доверительную вероятность =0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше . На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение , то этот результат считается промахом и исключается из ряда измерений.

Пример. Для известного числа измерений получены значения и . Определить вероятность того, что имеет место неравенство 1,261,28.

Так как , то 0,01/0,025=0,4. Используя таблицу интеграла вероятности, находим . Следовательно, около 30% общего числа измерений будут иметь случайную погрешность , не превышающую ±0,01.

Распределение Стьюдента

При малом числе повторных измерений 20 используется распределение случайных погрешностей, предложенное Стьюдентом. Плотность вероятности по этому закону зависит от значения случайной погрешности и от числа измерений:

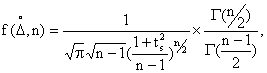
где (,)-плотность вероятности случайной погрешности при заданном числе измерений ; -гамма-функция; s=/ - коэффициент Стьюдента (“кратность” случайной погрешности).

На рис.1.11 показаны графики кривых распределения случайных погрешностей по закону Стьюдента для двух значений . При →∞ распределение Стьюдента совпадает с нормальным, а при 20 всё более и более от него отличается.

Доверительный интервал и доверительная вероятность s также зависят от числа измерений. Соответствующие значения s при заданном значении и приводятся в таблицах.

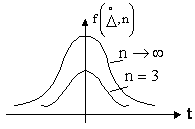
Рис.1.11

Коэффициент Стьюдента s определяется из соотношения s= =,где -СКО ряда измерений, -доверительный интервал.

Пример. Для числа измерений =6 среднее арифметическое значения =35,4, а СКО ряда наблюдений. Определить доверительную вероятность s , если отличается от истинного значения на величину доверительного интервала т.е. 35,2≤35,6.

Определим коэффициент Стьюдента s==.По таблицам распределения Стьюдента находим = 0,9. Следовательно, случайная погрешность результата измерения в 90% случаев не выйдет за пределы доверительного интервала.