Поможем написать любую работу на аналогичную тему
Чаще всего ряды ПЧ строятся на основе геометрической прогрессии, реже на основе арифметической прогрессии. Кроме того, есть разновидности рядов построенных на основе золотого сечения, двоичные ряды, комплементарные ряды и. т.д.
Ряды, построенные по арифметической прогрессии, характеризуются тем, что разность (интервал) значений двух соседних членов остается неизменной во всем диапазоне ряда, т.е.
, (4.1)
где 
– значения рядом стоящих членов ряда;
– разность (интервал) значений между двумя смежными членами ряда.
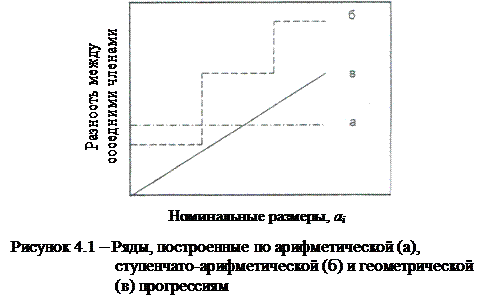
На рисунке 4.1 этот ряд показан прямой а. Арифметический ряд прост, не требует округления чисел, но его существенным недостатком является относительная неравномерность. При постоянной абсолютной разности относительная разность с увеличением номера члена ряда резко уменьшается.
Например: 1,2,3,…,9,10 относительная разность для чисел 1,2 составляет 100%, а для членов ряда 9,10 – всего 11%
Недостаток заключается в то, что наблюдается нецелесообразная разреженность значений в зоне малых величин и сгущенность их в зоне больших величин. Поэтому чаще применяются ступенчато-арифметические ряды, показанные на рисунке 4.1 б, т.е.
, (4.2)
где 
— первый член ряда;
— разность прогрессии;
— номер искомого числа.
На основе арифметических рядов, построены стандарты:
1) ГОСТ 87.24 – Резьба метрическая
Например: Ø 1,2…2,5 мм-d=0,2 мм
Ø 2,5…6,0 мм-d=0,5 мм
Ø 7,0…12,0 мм-d=1мм
2) ГОСТ 3478 Подшипники качения. Разность между смежными размерами внутреннего диаметра от
Ø 1…3 мм-d=0,5 мм
Ø 3…10 мм-d=1,0 мм
Ø 10,12,15,17-d=2,3 мм
Ø 20-d=5 мм
3) ГОСТ 9563 Колеса зубчатые. Модули.
| Предыдущие материалы: | Следующие материалы: |