Зависимость погрешностей от значения измеряемой величины Х.

Главная страница ---> Конспект лекций по дисциплине «метрология и радиоизмерения» ---> Зависимость погрешностей от значения измеряемой величины Х.

     По характеру зависимости от измеряемой величины погрешности можно разделить на аддитивные  (не зависящие от Х, лат. additivus - придаточный,

получаемый путем сложения) и мультипликативные (зависящие от Х, лат. multiplicatio - умножение).

     Такая погрешность называется аддитивной.

     Примером может служить погрешность, связанная с неточной установкой нуля стрелочного прибора. Аддитивная погрешность постоянна во всем диапазоне измерений, в том числе и при Х=0, поэтому ее часто называют погрешностью нуля.

где b - постоянная величина (для линейной погрешности и переменная величина при нелинейном характере погрешности); - предельное значение мультипликативной погрешности; a - это предельное значение аддитивной погрешности.

    

     Таким образом, мультипликативная погрешность прямо пропорциональна значению Х. (см.рис.9).

     

                               Нормирование погрешности прибора.  

    Приведенная (нормированная) аддитивная погрешность может быть записана в виде  

            (27)                     

- конечное значение диапазона измерений.

     Если:

1)

2)

3)                                                        (29)

4)                                                           (30)

Пример: Универсальный мост Е7-4 имеет основную относительную

погрешность при измерении (в %):

      - сопротивления на частоте 100Гц,

                                  0,1106                            0Гц,                  

- емкости С

                    10102                          1000Гц,            

-     индуктивности L

- добротности Q

                              130                    1000Гц,              

                                                 100Гц. 

     Поведение аддитивных и мультипликативных погрешностей с изменением измеряемой величины и их влияние на характеристику преобразования показано на рис.10

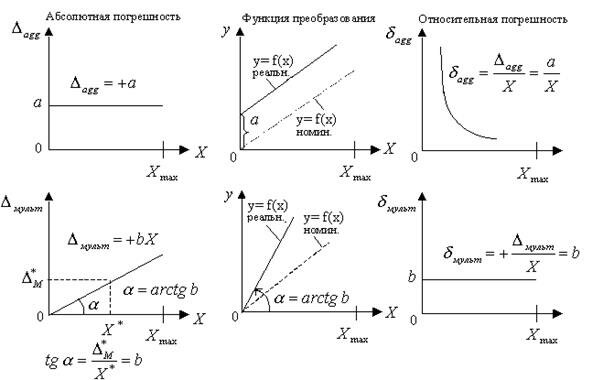
                                                        Рис.10

     Формулы вида (27) и (28) используют при нормировании погрешностей средств измерения. Погрешности средств измерений при нормировании округляют до двух значащих цифр и выбирают равными ближайшему числу из следующего ряда: 1×10n ; 1,5×10n ; 2×10n ; 2,5×10n ; 4×10n ; 5×10n ; 6×10n  (n=1,0,-1,-2…).

     Разработаны условные обозначения классов точности, которые применяются в документации, а также наносятся на шкалы средств измерения.

2. относительной.

3. абсолютной.

Форма выражения основной погрешности	Расчет допускаемой основной погрешности по формуле	Пределы допускаемой основной погрешности %	Обозначение класса точности на шкале прибора
			в доку-ментации	на приборе
Приведенная основная погрешность (предельная)	для СИ с равномерной шкалой- нормирование по пределу шкалы для СИ с неравномерной шкалой и нормирование производится по длине шкалы.	Примеры: %	Класс точности 0,5 1,5 0,5		% %	Класс точности 0,5 Класс точности 0,02/0,01 0,02/0,01	или по более сложной формуле	Пример1, 2 (см. после таблицы 6).	Класс точности М	М

1) С какой абсолютной погрешностью можно измерить на этом приборе напряжение 220В?

а) Обозначение 1,0 означает основная приведенная предельная погрешность %

б)   Предельная приведенная погрешность (по формуле (27))

%. Отсюда абсолютная погрешность

в)    Результат измерения    

2) Какова относительная погрешность, если измерять 10В? 150?

Основная относительная погрешность на этом диапазоне ( согласно формуле (28))

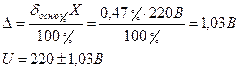
     Вывод: на цифровых вольтметрах измерение выполняется с большей точностью.